细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
如图,已知三角形ABC内角于圆O,角BAC=120度,AB=AC,BD
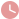

如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O
答案 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则BC= 6 A C B D 0 [考点]圆周角定理;解直角三角形 [分析]由已知可证∠BDA=30°;根据BD为⊙O的直径,可 如图,三角形ABC内接于⊙O,角BAC=120度,AB=AC,BD为⊙O的直 如图,三角形ABC内接于⊙O如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O与点D,连接BD,DC 若圆O的半径为10cm,角BAC=120度求三角形BAC面积的最大值如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分 2013年2月22日 — 如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D,DE垂直AB于E百度知道 1求证AE=AC+BE2若BE=AC=2,sin角BAD=2/5根号5,求圆O的半径帮帮 如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D,DE垂直AB于
.jpg)
如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O
2009年3月15日 — 外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。 ③R=2S 2012年12月9日 — 如图,已知三角形ABC内接于圆O,角C=45度,过点O作OD垂直AB于点D,OD=2,求弦AB分圆O所成的两条弧的长。 连接OA 如图,已知三角形ABC内接于圆O,角C=45度,过点O作OD垂直AB于 2014年5月2日 — 如图,已知三角形abc是圆o的内接三角形,ab=ac,点p是弧ab的中点,连接pa,pb,pc解:(1)∵∠BPC=60°, ∴∠BAC=60°, ∵AB=AC, ∴ ABC为等边三角形, 如图,已知三角形abc是圆o的内接三角形,ab=ac,点p是弧ab 2014年2月23日 — 简单的数学问题如图,三角形abc内接于圆o,ab等于bc,角abc等于120度,ad为圆o的直径解:∵AB=BC,∠ABC=120° ∴∠C=(180°120°)÷2=30° ∴∠D=30° ∵AD 简单的数学问题如图,三角形abc内接于圆o,ab等于bc,角abc等于120

已知: ABC是⊙O的内接三角形,AB=AC,在∠BAC所对弧
试题解析: (1)∠ADB=90°-; (2)延长BD到E,使得DE=DC,∵BAC=60°,AB=AC,∴ ABC是等边三角形,∴BC=AC,∠BAC=∠ACB=60°,∵四边形ABCD内接于 因为直径所对的圆周角是直角,所以作辅助线:连接AD;利用同角的余角相等,可得∠BAG=∠D,又由同弧所对的圆周角相等,可得∠C=∠D,证得∠C=∠BAG,又因为∠ABG 已知:如图, ABC是⊙O的内接三角形,⊙O的直径BD交AC于 2014年9月17日 — (2014?常德)如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80∵ ABC三个内角的平分线交于点O,∴∠ACO=∠BCO,在 COD和 COB中,CD=CB∠OCD=∠OCBCO=CO,∴ COD≌(2014?常德)如图,已知 ABC三个内角的平分线交于点O 为帮助你解决这道题,我将一步步引导你如何攻克它注意学习解决问题的方法1先在草稿纸上画一遍图,对所给条件有个简单印象2从问题入手,题目证 AB垂直平分DF3想象一下垂直平分相关的,再结合图,你便知道假如我证明到三角形BDF是等腰直角三角形而BG是1如图所示,在Rt三角形ABC中,角ACB=90度,AC=BC,D为BC
.jpg)
如图所示,在 ABC中,∠BAC=120°,AD平分∠BAC交BC于
2009年8月27日 — 如图,在三角形ABC中,角BAC=120度,AD平方角BAC 8 在三角形ABC中,角BAC=120度,AD平分角BAC角BC 如图三角形abc中,角bac=120度,ad平分角bac,交 19 如图,在 ABC中,AD平分∠BAC,交BC于2012年10月11日 — ab=ac 角bac=120度 所以角abc=角acb等于60度 所以角edca等于30度 由30度所对的边等于斜边的一半加上勾股定理即可算出ce 也可以得出ac 做垂线垂直于bc再次利用由30度所对的边等于斜边的一半加上勾股定理(或者正余弦函数)即可算出bc也就已知如图三角形ABC中,AB=AC,角BAC=120度,DE垂直平分 如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为 (3分)如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=92°,则∠BCA的度数为 42° A yeoo 如图,已知 ABC三个内角的平分线交于点O,点D在CA的 2013年1月7日 — 已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交边DC于点E,联结BD证明:因为AD是角BAC的角平分线所以:角BAD=角DAC因为:角DBC与角DAC都是狐DC所对的角所以,角DAC=角DBC 所以,角BAD=角DBC 所以,三角形BDE已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交

如图,已知三角形ABC内接于圆O,角C=45度,过点O作OD垂直
2012年12月9日 — 如图圆o是三角形abc的外接圆,ab为直径,od平行bc交圆 24 如图,在 ABC中,AB=AC,以AB为直径作⊙O,交BC于 25 如图,已知三角形ABC内接于⊙O,角C=45°,弦AB的弦心 15 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点D,OA2014年1月7日 — 如图三角形ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O的直径,AD=6,求DC长因为三角形ABC中,角BAC=120度,且AB=AC,所以角ABC=角BCA=30度,所以角BDA=30度,又因为BD是圆的直径,所以角BAD=90度,再因为角BDA=角BCA=30 百度首页 如图三角形ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O的 2007年4月16日 — 圆O半径为1,其内接一个三角形ABC,其中角A=60度,求此三角形的面积。取120°圆心角所对的弦为此三角形的一条边,在圆周除了这段弧长之外的部分上取一点A,自点A向此弦的两端引两条线段,组成的三角形中∠A=60°。当圆O半径为1,其内接一个三角形ABC,其中角A=60度,求此 2014年9月6日 — 已知:如图, ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O的直径解:如右图所示,连接OB、OC,并过O作OD⊥BC于D,∵OD⊥BC,BC=12,∴BD=CD=6,∵∠A=60°,∴∠BOC=120°,∵OB=OC,OD⊥BC,∴∠BOD=∠COD=60 已知:如图, ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O

如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D
2013年2月22日 — 如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D,DE垂直AB于E1)延长AB到F,使得BF=AC,连DF,CD因为AD平分BAC所以∠BAD=∠CAD所以BD=CD因为∠FBD=∠ACD,BF=AC所以 BDF≌ CDA所以DF=DA因为DE⊥AF所以EF=AE,因为EF=EB+2011年11月2日 — 如图,在三角形ABC中,AB=AC,角BAC=120度,AC的垂直平分线EF交AC于点E,交BC于点F,求证:BF=2CF证明:连接AF∵EF是AC的垂直平分线∴AF=CF∵∠BAC=120°,AB=AC∴∠B=∠C=30°∴∠C=∠CAF=30°∴∠BAF=90 如图,在三角形ABC中,AB=AC,角BAC=120度,AC的 如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA 1试求角DAE的度数 2如果把试题中AB=AC的条件去掉,其余条件不变,那么角DAE的度数会改变吗?为什么?如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上 2010年1月17日 — 已知 如图三角形ABC中,AB=AC,角BAC=90度当且仅当BD为角ABC的角平分线时CD=1/ 2BE延长CD与BA的延长线交于F 显然EDFA四点共圆=>角AEB=角CFA AB=AC 已知 如图三角形ABC中,AB=AC,角BAC=90度百度知道

如图,四边形ABCD为⊙ O的内接四边形,且AC为⊙ O的直径
3.如图,四边形ABDC是圆O的内接四边形,AD是对角线,过点A作EA⊥AD交DB的延长线于点E,AB=AC.(1)求证:∠ABE=∠ACD.(2)连接BC,若BC为圆O的直径,求证: ABE≌ ACD.A EB CD2013年9月15日 — 如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O于点D,连接BD,DC1求证:BD=DC=DI2若圆O的半径为10厘米,角B 如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O于点D,连接BD,DC如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的 2010年6月3日 — 如图,已知三角形ABC内接于圆O,AB=AC=5,BC=8,求圆O的半径长连A0并延长交BC于M因为; AB=AC 弧AB=弧AC又因为;AO过圆心所以; AM垂直并平分BC所以; BM=CM=4又因为;直角三角形BMO 所以; B0的平方+MO的平如图,已知三角形ABC内接于圆O,AB=AC=5,BC=8,求圆O的 2018年4月24日 — 已知: ABC外接于圆O,∠BAC=60°,AE⊥BC,CF垂直AB。AE、CF相交于点H,点D为弧BC的中点。连接HD,AD。求证: AHD为等腰三角形。 已知: ABC外接于圆O,∠BAC=60°,AE⊥BC,CF垂直AB。已知: ABC外接于圆O,∠BAC=60°,AE⊥BC,CF垂直AB
.jpg)
如图,⊙O为 ABC的外接圆,∠BAC=60°,H为边AC,AB上
2016年12月1日 — 如图,⊙O为 ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上取点M,使BM=CH.(1)求证:∠BOC=∠BHC;(2)求证: BOM 如图,⊙O为 ABC的外接圆,∠BAC=60°,H为边AC,AB上的高BD,CE的交点,在BD上 如图,已知AB是半径为1的圆O的一条弦,且AB=a<1,以AB为一边在圆O内作正三角形ABC,点D为圆O上不同于点A的一点,且DB=AB=a,DC的延长线交圆O于点E , 百度试题 如图,已知AB是半径为1的圆O的一条弦,且AB=a<1,以 如图,在三角形ABC中角C等于90度,AC=BC,AD平分角BAC求证:AC+CD=AB 要用补短的方法 百度试题 结果1 结果2 结果3 题目 如图,在三角形ABC中角C等于90度,AC=BC,AD平分角BAC求证:AC+CD=AB 如图,在三角形ABC中角C等于90度,AC=BC,AD平分角BAC 2013年12月19日 — 如题AB=AC,∠BAC=20,∠BDC=30得到∠ACD=10°与等边对等角相矛盾。 若AB=AC,∠A=20°,AD=BC。求得∠BDC=30°。解:过A点作CD的垂线交CD的延长线于点E,作AF⊥BC,垂足为F。 在 AEC和 CFA中 ∵∠E=∠AFC=90°∠ECA=∠FAC,AC=AC如图,三角形ABC中,AB=AC,∠BAC=20,∠BDC=30,求证
.jpg)
在三角形ABC中,角BAC=120度,以BC为边向形外作等边三角
2013年6月6日 — 题目应该是这样的吧: 如图,在 ABC中,∠BAC=120°,以BC为边向外作等边 BCD,把 ABD绕点D按顺时针方向旋转60°后到 ECD的位置。若AB=3,AC=2,求∠BCD的度数和AD的长。已知:如图,在 ABC中,AB=AC,点D,E分别在边AC,AB上,且∠ ABD=∠ ACE,BD与CE相交于点O求证:(1)OB=OC;(2)BE=CD (1)证明:∵AB=AC, ∴∠ABC=∠ACB; ∵∠ABD=∠ACE, ∴∠OBC=∠OCB, ∴OB=OC (2)证明:如图, A E D 已知:如图,在 ABC中,AB=AC,点D,E分别在边AC 如图,三角形ABC中,AB=AC,角BAC等于120度,EF是AB的垂直平分线,EF交BC于F,交AB于E求证BF=二分之一FC 如图所示, ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.如图在 ABC中,AB=AC,∠BAC=120°,EF为AB的垂直 (1)延长AO交BC于H,连接BO,证明A、O在线段BC的垂直平分线上,得出AO⊥BC,再由等腰三角形的性质即可得出结论;(2)延长CD交⊙O于E,连接BE,则CE是⊙O的直径,由圆周角定理得出∠EBC=90°,∠E=∠BAC,得出sinE=sin∠BAC,求出CE=如图, ABC内接于⊙ O,AB=AC,CO的延长线交AB于点D

如图 在三角形abc中,AD是角BAC的平分线,E、F分别为AB
2019年1月26日 — 求证DE=DF证明:过D作DM⊥AB,于M,DN⊥AC于N,即∠EMD=∠FND=90°,∵AD平分∠BAC,DM⊥AB,DN⊥AC,∴DM=DN (角平分线性质 百度首页 商城 注册 登录 资讯 视频 图片 知道 文库 贴吧 采购 地图 更多 答案 我要提问 如图 在三角形abc 2009年10月8日 — 如图所示,圆O是 ABC的外接圆。角ABC与角BAC的平分线相交于点I。延长AI交圆O于点D,连结BD、DC1∵∠ABC与∠BAC的平分线相交于点I,∴∠BAD=∠CAD,而C⌒D所对圆周角是∠CAD,∠CBD,∴∠CAD=∠CBD,同理,∠BAD=∠BCD, 百度首页 如图所示,圆O是 ABC的外接圆。角ABC与角BAC的平分线 2018年4月12日 — 在三角形ABC中,AB=AC,角A=100度,BD平分角ABC求证:AD+BD=BC解:∵∠A=100° 且AB=AC∴∠ABC=∠ACB=40°又∵DB平分∠ABC ∴∠ABD=∠DBC=20°且∠ADB=60° 延长BD到E点,使DE=AD,在BC上找一点F,使BF=AB得 在三角形ABC中,AB=AC,角A=100度,BD平分角ABC求证 2017年11月26日 — 如图,三角形ABC中,AB=AC,角BAC=54度,角BAC的平分线与AB的垂直平分线交于点O,将角C沿EF(E在BC上,F在AC 上)折叠,点C与点O恰好重合,则角OEC为多少度? 展开如图,三角形ABC中,AB=AC,角BAC=54度,角BAC的平分线

如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC
如图,四边形 内接于圆, ,对角线 平分 E AD CB(1)求证: 是等边三角形;(2)过点 作 交 的延长线于点 ,若 ,求 的面积2012年3月21日 — 解:延长DC,AB交于点E,因为∠ECB=∠BAD=60°(圆内接四边形的外角等于它的内对角) ∠ABC=90° ∴∠EBC=90° ∴∠E=30° ∴EC=2BC=2×3=6 ∴EB=√(3)BC=3√(3) ∴ED=DC+EC=5+6=11如图,四边形ABCD内接于圆O,角BAD=60,角ABC=90,BC=3 2009年9月2日 — 在三角形ABC内角BAC=60°角ACB=40°PQ分别在BCCA上 APBQ分别为角BAC、角ABC的平分线 。求BQ+AQ=AB+BP 证明: 做辅助线PM‖BQ,与QC相交与M。(首先算清各角的度数)已知在 ABC内,∠BAC=60°,∠C=40°,PQ分别在BC,CA上,且 2015年2月4日 — 如图所示,圆O是 ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于点D,连接BD、DC.(1)求证:BD=DC=DI;(2)若圆O的半径为10cm, 如图所示,圆O是 ABC的外接圆,∠BAC与∠ABC的平分线相交于点I,延长AI交圆O于 如图所示,圆O是 ABC的外接圆,∠BAC与∠ABC的平分线
.jpg)
如图所示,三角形ABC内接于圆O,AB是圆O的直径,点D
2011年3月12日 — 三角形OBC是正三角形,所以{OC=BC,角AOC=角DBC=120度,角A=角D};所以三角形AOC全等于三角形 如图所示,三角形ABC内接于圆O,AB是圆O的直径,点D在AB的延长线上,角A等于角D等于30度,判断DC是否为圆O的切线,说明理由 2016年12月2日 — 三角形ABC的外角角ACD的平分线CP与内角角ABC的平分线BP交于点P,已知角BPC=40度。(1)若角ABC=角ACB,则角BAC=?(要步骤)(2)求角CAP的度数 三角形ABC的外角角ACD的平分线CP与内角角ABC的平分线BP交于点P,已知 三角形ABC的外角角ACD的平分线CP与内角角ABC的平分 如图,已知在三角形ABC中,AB=AC,角BAC=120度,AC的垂直平分线EF交AC于点E,交BC于点F,求证BF=2CF 如图,在三角形ABC中,AB=AC,角BAC=120°,AD是BC边上的中线,且BD=BE,CD的垂直平分线MF交AC于点F,交BC于点M,MF的长为2已知:如图,在 ABC中,AB=AC,∠BAC=α,且60°<α 【答案】分析:由AB+BD=DC,易想到可作辅助线DE=DB,然后连接AE,从而可出现两个等腰三角形,一个是 ABE,一个是 ACE,利用三角形外角的性质,易求∠B=2∠C,再利用三角形内角和定理可求∠C. 解答: 解:在DC上截取DE=DB,连接AE,设∠C=x,∵AB+BD=DC,DE=DB,∴CE=AB,又∵AD⊥BC,DB=DE,如图,在 ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD

如图, ABC内接于⊙O,∠BAC=120°AB=AC,BD为 ⊙O的
2007年12月30日 — 如图, ABC内接于⊙O,∠BAC=120°AB=AC,BD为 ⊙O的直径,AD=6,则BC= 。 ,连接OA O为圆心因为AB=AC 所以 ABC为等腰 ∠BAC=120°所以∠ACB=∠ABC=30°所以∠ADB=30° 定理不记得了因为OA=OD那么 OAD为等腰如图,已知三角形ABC中,角BAC=90度,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD垂直AE于D,CE垂直AE于E,试说明:BD=DE+CE 百度试题 结果1如图,已知三角形ABC中,角BAC=90度,AB=AC,AE是过A的一 2014年9月17日 — (2014?常德)如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80∵ ABC三个内角的平分线交于点O,∴∠ACO=∠BCO,在 COD和 COB中,CD=CB∠OCD=∠OCBCO=CO,∴ COD≌(2014?常德)如图,已知 ABC三个内角的平分线交于点O 为帮助你解决这道题,我将一步步引导你如何攻克它 注意学习解决问题的方法 1先在草稿纸上画一遍图,对所给条件有个简单印象 2从问题入手,题目证 AB垂直平分DF 3想象一下垂直平分相关的,再结合图,你便知道 假如我证明到三角形BDF是等腰直角三角形而BG是顶点B的角平分线 问题不就解决了?1如图所示,在Rt三角形ABC中,角ACB=90度,AC=BC,D为BC

如图所示,在 ABC中,∠BAC=120°,AD平分∠BAC交BC于
2009年8月27日 — 如图,在三角形ABC中,角BAC=120度,AD平方角BAC 8 在三角形ABC中,角BAC=120度,AD平分角BAC角BC 如图三角形abc中,角bac=120度,ad平分角bac,交 19 如图,在 ABC中,AD平分∠BAC,交BC于2012年10月11日 — ab=ac 角bac=120度 所以角abc=角acb等于60度 所以角edca等于30度 由30度所对的边等于斜边的一半加上勾股定理即可算出ce 也可以得出ac 做垂线垂直于bc再次利用由30度所对的边等于斜边的一半加上勾股定理(或者正余弦函数)即可算出bc也就已知如图三角形ABC中,AB=AC,角BAC=120度,DE垂直平分 如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=80°,则∠BCA的度数为 (3分)如图,已知 ABC三个内角的平分线交于点O,点D在CA的延长线上,且DC=BC,AD=AO,若∠BAC=92°,则∠BCA的度数为 42° A yeoo 如图,已知 ABC三个内角的平分线交于点O,点D在CA的 2013年1月7日 — 已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交边DC于点E,联结BD证明:因为AD是角BAC的角平分线所以:角BAD=角DAC因为:角DBC与角DAC都是狐DC所对的角所以,角DAC=角DBC 所以,角BAD=角DBC 所以,三角形BDE已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交
.jpg)
如图,已知三角形ABC内接于圆O,角C=45度,过点O作OD垂直
2012年12月9日 — 如图圆o是三角形abc的外接圆,ab为直径,od平行bc交圆 24 如图,在 ABC中,AB=AC,以AB为直径作⊙O,交BC于 25 如图,已知三角形ABC内接于⊙O,角C=45°,弦AB的弦心 15 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点D,OA2014年1月7日 — 如图三角形ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O的直径,AD=6,求DC长因为三角形ABC中,角BAC=120度,且AB=AC,所以角ABC=角BCA=30度,所以角BDA=30度,又因为BD是圆的直径,所以角BAD=90度,再因为角BDA=角BCA=30 百度首页 如图三角形ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O的 2007年4月16日 — 圆O半径为1,其内接一个三角形ABC,其中角A=60度,求此三角形的面积。取120°圆心角所对的弦为此三角形的一条边,在圆周除了这段弧长之外的部分上取一点A,自点A向此弦的两端引两条线段,组成的三角形中∠A=60°。当圆O半径为1,其内接一个三角形ABC,其中角A=60度,求此 2014年9月6日 — 已知:如图, ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O的直径解:如右图所示,连接OB、OC,并过O作OD⊥BC于D,∵OD⊥BC,BC=12,∴BD=CD=6,∵∠A=60°,∴∠BOC=120°,∵OB=OC,OD⊥BC,∴∠BOD=∠COD=60 已知:如图, ABC内接于⊙O,BC=12cm,∠A=60°.求⊙O
是钙粉料场还是石灰石方解石场
--上海方解石粉碎机械滑石
--高性能轮胎式碳酸钙粉碎站
--枞阳海螺水泥股份有限公司
--锂矿破磨设备巴马克雷蒙磨
--稀土矿粉碎设备
--煤灰磨粉机械多少钱一台
--青岛市石场开采程序
--碳酸钙粒级分级制
--园维矿石磨粉机型号
--粉体粉磨系统
--桂林鲲鹏雷蒙磨粉机
--加工粉末冶金厂
--找湖南能把石头粉碎成沙子的机器
--高岭土石灰石制粉生产线
--石灰石超细磨粉机
--上海好夫满
--分离纳米级煤粉需要多大的离心力
--九江湖口县文方解石厂
--自然煤矸石
--上海世博粉碎设备
--水渣选铁
--研磨岩石需要多大力量
--文化石废料矿石磨粉机
--zenith重工上海启东建设
--三头矿石磨粉机设备
--天津矿渣粉贸易商
--粉料仓结构图
--怎么解决针片状的问题
--上海益奔机械制造有限公司上海益奔机械制造有限公司上海益奔机械制造有限公司
--










